UC Berkeley
Abstract
How can designers of instructional materials for mathematics learning best support students' progress from intuition to inscription? This paper explains the embodied-design methodology for creating cognitively ergonomic learning tools. Two case studies are contrasted in which individual participants in a design-based research study of mathematical cognition engaged in problem-solving situations pertaining to the content of probability. I analyze the microgenesis of the reflexive, mediated interplay between students' multimodal, intuitive, presymbolic notions and the available multimedia tools (cf. Radford, 2003). The first case demonstrates how the interviewer-student dyad coped with the ontological imperialism (Bamberger & diSessa, 2003) inherent to some forms of notation. Following a brief overview of how embodied mathematical reasoning, and particularly gesture studies, can contribute to a deeper and more nuanced understanding of students' reasoning processes as they problem solve, I recount the second case, in which close listening to a student's truncated expressivity directly informed the design of a computer-based module that enables electronic gesture through which students can elaborate their reasoning and interlink spatial and symbolical referents. I advocate a measured balance between streamlined and frictive learning tools, because it is in breakdown that creative reasoning and creative habits of mind are fostered.
Keywords
1. Introduction
In inscribing—writing, drawing, notating—we project presymbolic notions into and through a representational system hosted in an available medium, thus rendering the phenomenological semiotic (Radford, 2003; Vygotsky, 1978/1930). Doing so, we are tacitly relying both on the availability of suitable media and on our basic fluency with representational systems. Yet what happens in the case of explorative problem solving, where requisite media are not necessarily at hand and representational systems are yet to be created let alone mastered? This paper tracks the evolution of a design rationale for supporting mathematical problem-solving processes in which media and representational systems emerge as negotiated products in a structured collaboration between a designer and research participants. In a sense, it is a design-theory paper on methodology for creative design enabling creativity.
Mathematical thinking is vacuous without the machinery of the mathematical semiotic system, be it embodied in the human body, oral tradition, or scripted notations, and this machinery is a cultural legacy into which individual cognizers are acculturated through participation in organized discourse-based practices (Cobb & Bauersfeld, 1995; Ernest, 1988; Gee, 1996; Lemke, 1998; Radford, 2003; Saxe, 1981; Wittgenstein, 1956). Yet, as Olson (1994) has argued, the inscribed is no neutral receptacle; the medium, or more precisely a person’s intentional representational interaction with the medium, participates in the construction, elaboration, and, at times, modification of the presymbolic experience (see also Rotman, 2000), such that “content“ and “form“ of mathematical thought become ontologically and epistemologically inextricable. In the hands of fluent agents in a semiotic system, this dynamic reciprocity of intuitive content and representational form may be advantageous to the development of source notions (for example, the word processor I am using to edit this text is facilitating my reasoning). However, this content–form reciprocity may challenge novices to a representational system, making for learning impediments and communication breakdowns. Whereas it would be absurd to critique the very idea of introducing learners into pre-existing representational systems - such a line of argument would imply a critique of teaching children to adopt natural language - this paper is intended to illuminate cases where careful design and facilitation may support students in experiencing a safer and more empowering passage from intuition to inscription, i.e., from “raw“ phenomenology to participation in cultural semiotic practice. Moreover, because the context of the studies discussed below is that of technological design in the service of learning, students participating in explorative usability testing contribute to the ongoing development of new mathematical artifacts. As such, designers and students are co-dependent partners in pedagogical creativity' the designer applies professional acumen to enable students to voice their incipient notions, but the designer cannot, in principle, anticipate all these emergent notions.
The contribution of this paper is in the suggestion, supported by empirical data, that in order to engender students' creative reasoning, we should attend very closely to what they are attempting to express, and where we detect the unavailability of optimal semiotic means of objectification (Radford, 2003), we should respond with design that enables the students to coalesce their burgeoning thoughts. Specifically, I will demonstrate how scrutinizing students' hand gestures from an embodied-cognition perspective informed the design of mixed-media pedagogical materials that I call cognitively ergonomic learning tools (Abrahamson, in 2008a). Thus, in submitting this paper to the CreativeIT workshop, I am implicitly arguing for a breadth of theoretical perspective in the study of creativity: the creative act, proverbially an individual's spark of de-situated genius, is inherently situated within a socio-cultural context and can be coconstructed by multiple agents (e.g., Sawyer, 2007). One such agent is a design-based researcher.
The data discussed in this paper were collected in the context of the Seeing Chance project (Abrahamson, 2006a, 2007b, in 2008b; Abrahamson & Cendak, 2006; Abrahamson & Wilensky, 2007), an investigation of students' problem solving in situations pertaining to the mathematical study of probability. These studies were conducted using the meta-methodology of design-based research, a paradigm, first explored in the late 1980's (Brown, 1992; Collins, 1992). Initially inspired by engineering practices and attempting to address the complexity of real learning ecologies, design-based research is now firmly established as a powerful approach to researching diverse cognitive and social phenomena occurring in learning environments through studying the iterative implementation of experimental materials and/or pedagogical practices (Barab et al., 2007; Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003; Confrey, 2005). The learning materials used in my studies are part of ProbLab (Probability Laboratory, Abrahamson & Wilensky, 2002), an under-development experimental middle-school unit that continues the Connected Probability project (Wilensky, 1997) and utilizes the NetLogo multi-agent modeling-and-simulation environment (Wilensky, 1999). The theoretical and pedagogical frameworks underlying ProbLab's unique design rationale as well as empirical findings from implementing the design are detailed elsewhere (e.g., Abrahamson, in 2008b); selected interactive materials are on http://edrl.berkeley.edu/ design.shtml.
I begin, below, by introducing the ProbLab learning materials used in these studies. Next, I present and analyze the case study of LF 'a middle-school student' that has been revealing to me deep dilemmas underlying constructivist design (for a critique of constructivist design that fails to deliver, see Kirschner, Sweller, & Clark, 2006). I will discuss the case of LF as demonstrating the ontological imperialism (Bamberger & diSessa, 2003) we are liable to impose on students, and how we must listen closely to students' voices (Confrey, 1991) in order to improve our design and teaching. Next, following a brief overview of the embodied-reasoning perspective on mathematical reasoning, I build on insight from the LF case to interpret the case study of MK'a college senior' whose close encounter with the obduracy of the world'the shortcoming of immediately available media to enable expression of an elaborate mathematical thought was detected through microgenetic video analysis (Siegler & Crowley, 1991) so that we could create new media tailored to her, and presumably other students', needs.
2. Design: Learning Materials for an Interview-Based Investigative Mini-Lesson in Basic Probability
Leading education researchers of probabilistic cognition generally agree as to the pedagogical value of enabling students to explore the complementarity of two inquiry activities, 'theoretical' and 'empirical,' targeted at random generators: (a) combinatorial analysis as an instrument for determining expected outcome distributions in actual experiments with the generators; and (b) experimentation, typically computer simulated (Jones, Langrall, & Mooney, 2007). ProbLab offers one plausible methodology for facilitating this theoretical-empirical complementarity.
ProbLab mathematical objects are embodied in mixed media - both traditional and computer-based. A researcher, working with a flexible interview protocol (Ginsburg, 1997), engages students in activities using ProbLab materials. The interview begins with students analyzing an experimental procedure in which four marbles are drawn out randomly from a boxful of mixed green and blue marbles of equal numbers. To draw out these samples, we use a special utensil, the marble scooper, consisting of four concavities arranged in a 2-by-2 array (a 4-Block; see Figure 1a). Thus, unlike classical urns from which we draw order-less samples, e.g., a combination of 1 green and 3 blue marbles that roll around in no particular order, the scooper has inherent structural order, such that any draw perforce is a particular permutation on the order-less combination, e.g., 'blue, green, blue, blue.' Students are asked to guess what the most common draw might be. According to probability theory, the most likely draw is the event, or combination, with exactly 2 green marbles and 2 blue marbles in any order. Specifically, the distribution of expected events by number of green marbles is 1:4:6:4:1, corresponding to 0 green, 1 green, 2 green, 3, green, and 4 green, respectively (these 16 outcomes are arranged, in Figure 1b, in a histogram-like distribution). Typically, middle-school students correctly predict the 2-green-blue sample as the most common draw and warrant this guess by referencing the 'half-half' distribution of green and blue marbles in the box (Abrahamson, 2007c; Abrahamson & Cendak, 2006). In stating their prediction, these students' who have not studied probability 'make no allusion to the order of the marbles in the scooper. Prompted, the students keep referring to their visual impressions and offer no analytic warrant.
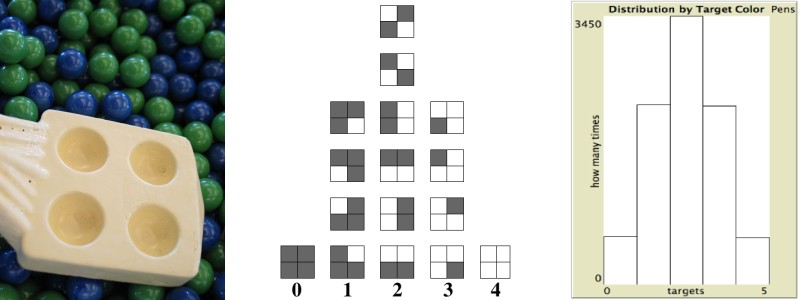
| a | b | c |
Figure 1. ProbLab materials used in the study's theoretical and empirical embodiments of the 4-Block mathematical object: (a) The marble scooper; (b) the combinations tower; and (c) an actual experimental outcome distribution produced by a computer-based simulation of this probability experiment.
Next, students are guided to use a set of stock-paper cards, each depicting an empty 4-block (a blank 2-by-2 grid) as well as green and blue crayons so as to create all the different 4-block patterns one could possibly draw out of the box with the scooper. This general procedure is called in probability theory combinatorial analysis, albeit the students may or may not be aware of the mathematical implications of the activity in which they are engaging. There are 16 unique green/blue configurations (24), yet if one does not attend to the order of the green and blue marbles in the samples, there are only five possible objects - 4 blue; 1 green and 3 blue, 2 green and 2 blue, 3 green and 1 blue, and 4 green (hence 0g-4b, 1g-3b, 2g-2b, 3g-1b, 4g-0b)- and these five events (appear to) exhaust "what you can get" when you operate the device
By way of a negotiation with the interviewers, all students eventually construct all 16 unique outcomes and are then guided to arrange these cards in columns by number of green cells in the 4-blocks. The result is the combinations tower (see Figure 1b), the sample space of the 4-block stochastic device that is distributed such that it anticipates the shape of things to come (Abrahamson, 2006b) in actual or simulated experiments with the random generator (see Figure 1c; by default, the computer simulations are set at .5 p value, reflecting the equal numbers of green and blue marbles in the box). This hybrid nature of the combinations tower - that it shares figurative properties with two constructs that students purportedly need to coordinate toward deep conceptual understanding, here a sample space and an experimental outcome distribution (compare Figures 1b & 1c - is a hallmark of the learning axes and bridging tools design framework for mathematics education (Abrahamson, 2004; Abrahamson & Wilensky, 2007).
Students who have worked with the combinations tower are then asked to describe outcome distributions they expect to receive in a computer-based probability experiment that simulates the operation of the 4-block stochastic device and accumulates the experimental outcomes according to the number of green in each scoop (the ProbLab 'Sample Stalagmite' model, Abrahamson, 2006b). We ask, "What will the histogram look like?"; "Now, what if we change the probability of getting green from .5 to a greater number?" As we will see in the data excerpts, students spontaneously elect to use the combinations tower, on the desk in front of them, so as to describe the outcome distribution they anticipate in a computer-based simulation. Thus the activity design creates opportunities for students to juxtapose the theoretical and empirical aspects of random process and, through supported insight, to coordinate them (Abrahamson, in 2008b; Abrahamson & Cendak, 2006).
We now turn to the case studies. In the first case study, LF negotiates with the interviewer modes of engagement with the combinations tower - the interviewer disciplines LF's perception (Stevens & Hall, 1998) toward the combinations tower such that LF comes to see the tower as representing anticipated results from running the marbles-box experiment. I will interpret LF's difficulty as a rupture caused by the unavailability of suitable semiotic means of objectification (Radford, 2003) that would enable him to reify his presymbolic psychological objects. In the second case study, MK attempts to use the combinations tower to express a prediction for an experiment with unequal numbers of green and blue marbles, but the medium falls short of conveying the message. Still within that round of research studies, though, we created a new computer-based module, Histo-Blocks, that appears to enable students to express that message, i.e., to concretize their envisioned manipulation of the combinations tower, if virtually.
3. A Case of Ontological Imperialism Causing Inadvertent Metonymy, or, "Try to See Things My Way, Do I have to Keep on Talking Till I Can't Go on? While You See It Your Way(We Can Work It Out!)"
Gazing at the box (see Movie 1), LF concluded that '2g-2b' would be the most common draw. He then works with the empty 4-block cards. He builds the five possible events (see Figure 2, on the right, the bottom row) and is content that they exhaust the sample space, e.g., LF sees the card that has a single light-colored square in the top-right corner as objectifying the 1g event (LF inadvertently sees the outcome as metonymical of an entire event class). The interviewer, however, perceives this same card as objectifying one particular permutation out of all four possibilities (see, in Figure 2, three additional grayed out permutations above that card). That is, the card is an ambiguous or polysemous semiotic object, and the dyad tacitly disagrees over its meaning - whether it is an event or an outcome. LF does not initially realize the implications of his representation' that he has unwittingly been subjected to ontological imperialism (Bamberger & diSessa, 2003) through interacting with the media put at his disposal as expressive means. That is, LF is not aware that by virtue of using the available media, he has represented his intuitive judgment such that a skilled user of the medium reads into the representations meanings, new layers of signification, that LF had not intended or even harbored. Namely, the emergent cues are 'visible' only to practitioners in this disciplinary domain (see Goodwin, 1994, on 'professional vision'), for whom order counts in combinatorial analysis. Thus, the available semiotic means of objectification were coerced upon LF. His presymbolic categories were order-less combinations, and yet the cards' structural properties add specificity, rendering order-less combinations ordered permutations. LF was seeing combinations as the 'things' in the experiment, yet the media imposed upon him permutations as the privileged elemental unit.

Figure 2. "These don't really matter" (+ gesture): the sample space, as the student initially sees it.
The cards appear to the interviewer (hence, Int.) as outcomes, because he is attending to the particular configuration of little squares (the four independent outcomes), whereas LF is not. Yet attending to order is the core learning issue of this analytic process LF is to master. To these ends, the order/no-order ambiguity is designed into the mathematical objects precisely so as to foster an opportunity for the student to discover that this property of order is a pertinent semiotic means of warranting the initial intuitive judgment (i.e., that 2g-2b would be the most common draw). Also, Int. was expecting LF to build 16 cards the complete sample space that includes all the permutations and so Int. interpreted the 5 cards not only as representing the 5 possible events (combinations) but also as an incomplete set of outcomes (permutations). However, as the ensuing conversation reveals, LF sees the cards as events, because his communicative goal (representational intention) is to objectify the presymbolic notion that corresponds to events, not outcomes. For LF to attend to order, the dyad must first acknowledge their differing orientations of view (Stevens & Hall, 1998) toward the cards, objectify and name these orientations, and then negotiate whether one of the orientations is more advantageous toward achieving the common goal. Yet, this goal - applying combinatorial analysis to determine expected experimental outcomes (i.e., showing 'what we could get' so as to determine 'how often we will get it') - itself is emergent for LF. For him, perhaps, the process of building the five cards appears as no more than an opportunity to reiterate his earlier statement, using semiotic objects conducive to deixis. That is, LF does not initially know that by attending to order he can create a set of objects, the sample space, that would collectively index his presymbolic notion. The complete mathematical pertinence of the combinatorial analysis procedure is thus temporarily suspended - the procedure will be instrumentalized (Vérillon & Rabardel, 1995) only once LF sees the sample space (the product of this procedure) in its entirety as indexing his presymbolic notion; only once LF objectifies (Radford, 2003) the combinations tower as resonant with his intuitive judgment; only once he blends (Fauconnier & Turner, 2002; Hutchins, 2005) the unarticulated sense of frequency into the 16 cards; only once he synthesizes the intuitive and formal (Schön, 1981). Thus the goal of the activity of coloring the cards is telescopically enfolded into their 'hidden' property of order.
Interactions such as LF and Int. experienced could be interpreted as creating confusion and hence injurious to the learning trajectory. Yet, I propose, these moments can be regarded alternatively as necessary transitional psychological states most amenable to the appropriation of cultural artifacts. That is, given a viable semiotic means of elaborating on the five cards such that they connote the mathematically normative presymbolic qualitative distribution, LF is likely to appropriate those means. One could imagine a variety of such semiotic means, e.g., using a red marker to indicate upon the five cards the 'intensity' of their respective felt likelihoods, yet only combinatorial analysis offers a semiotic means in line with the cultural practice of mathematical argumentation; once constructed, the columns of the combinations tower anchor the felt frequencies as five vertical projections and, in so doing, render the qualitative notion quantitatively explicit. Moreover, I propose, LF possibly needed to objectify the sample space piecemeal - first the objects (combinations), then their properties (frequency) - in order to render the phenomenological object– property compound semiotic. Indeed, through interacting with the interviewer, LF will come to regard the sample space as a means of recording his felt sense of relative frequency. Yet, en route to understanding, as we shall see, LF himself is affected reflexively by the emerging meanings of the mathematical object he created - LF enters a transitional phase of generative confusion, as follows.
Gazing at the five cards he had just created, LF retracts his initial intuitive judgment, stating that the five events are equally likely to occur [sic!]. To the extent that LF's representational intention had been to objectify frequency distribution, he has concretized the 'what' (the five events) but not their 'how often' (frequency) - the objects he had created are now laid out for his inspection but their properties had not been inscribed. Perhaps LF still entertained those properties for a fleeting moment, blending them into the cards, but then, as in a Stroop effect of sorts, the immediate perceptuality of the cards, semiotically undifferentiated as they were one from another with respect to their expected frequencies, superceded the presymbolic notion - in the absence of any such qualification, the cards appeared equal. Just as the 4-block structure of the cards compelled an ordered display of an orderless notion, so now the cards' lack of affordance for marking frequency engendered the apprehension of a flat distribution. It is as though LF has unburdened the onus of information onto the cards and now, gazing afresh, trusts the cards to re-evoke that presymbolic notion. Thus, crucial aspects of a presymbolic notion are attenuated once the notion is mirrored through a person's constrained fluency with a representational system, breeding conflict between the intuitive and the inscribed. How can this conflict be resolved? What can a teacher do to mediate conflict resolution?
Int.'s objective becomes to enable LF to regain and sustain his presymbolic sense of the distribution by appropriating semiotic means of objectification in keeping with mathematical convention and validity. He asks LF to create the permutations on the five combinations. Somewhat reluctantly, LF builds the remaining 11 cards, yet he objects that the permutations are not pertinent to the analysis, because the initial question was about events, not outcomes (see Figure 2). Then, upon further observation, he sees the middle column as implying a 6/16 chance for that 2g-2g event. It is as though LF has "shifted gears" and is now building an analytic argument in a mental space that temporarily cordons off the event-based intuition that had been so robust. Yet as his gaze shifts to other parts of the combinations tower, specifically to the 4g single-outcome event, LF reasserts his flat-distribution hypothesis. In response, the interviewer prompts LF to re-consider the marbles box, thus re-evoking for LF the activity's initial context. LF experiences resonance between the sample space and his initial intuition: he sees the columns' relative heights or counts as indexing the anticipated plurality of 2g-2b (see Abrahamson, Bryant, Howison, & Relaford-Doyle, 2008, for further case analyses).
LF's passage from intuition to inscription, though ostensibly complete, was a bumpy passage that may have left scars on the traveler. Though a logical, procedural, perceptual string does connect LF's presymbolic intuition to the interpreted sample space, this string is quite threadbare, perhaps leaving LF in a state that Wilensky (1997) calls epistemological anxiety, i.e., knowing that you know how to work something but not knowing why it works the way it works. A radical implication of the above would be that students are to be given all the leisure, latitude, and learning materials needed to create their own idiosyncratic representations of their intuitive notions - to create their personal paths from intuition to inscription (Abrahamson, 2007a), from phenomenology to semiosis. Yet, the necessity of shared semiosis (not to mention the assessment-based exigencies of the school context) appears to deem such a position impractical. Indeed, a common misunderstanding of radical constructivism is that children are left as "free range agents in the learning environment (von Glasersfeld, 1992). The question evoked by the LF data, then, is how to foster students' reflective negotiation between their presymbolic notions and the target semiotic systems they are to learn, e.g., how to ethically establish a sample space as the epistemic form for predicting random distribution; and combinatorial analysis as the epistemic game (Collins & Ferguson, 1993) one must play to construct this form. The key, I believe, reinterprets the constructivist caveat of departing from where the students are - we are to grasp what the students are trying to express as they engage in problem solving. Such insight into students' presymbolic notions can be enhanced by attending not only to their utterance and inscription, but to their entire multimodal, multimedia, multi-system embodied behavior. Doing so, we may be better able to determine what semiotic means of objectification students need that we are to design. Following a theoretical elaboration on the above, we will return to the data.
4. Close Listening to Gesture: An Embodied-Design Perspective on Mathematical Reasoning
I depart from a premise, grounded in phenomenological philosophy and cognitive-science research, that embodied mechanisms - including kinesthesia, visuo-spatial images, audiated sound, proprioceptive motorics, etc. - are constitutive of reasoning, i.e. they are not mere epiphenomena of some would-be proposition-based symbol-processing reasoning (e.g., Barsalou, 1999; Goldin, 1987; Merleau-Ponty, 1992; Rizzolatti & Arbib, 1998; Varela, Thompson, & Rosch, 1991). One window onto such embodied mechanisms is gesture. Gesture - aspects of hand/arm motion that do not physically manipulate utensils or the environment - is associated with dedicated aspects of reasoning that may not be communicated through verbal utterance (e.g., Kendon, 2004; McNeill, 1992; Radford, 2003; Schegloff, 1984). I focus on gesture in the context of mathematical learning and practice.
Gestures people perform as they reason about mathematical problems are informative of the multimodal resources they are bringing to bear (e.g., Alibali, Bassok, Olseth, Syc, & Goldin-Meadow, 1999). In particular, gesture acts as a unique window onto reasoning associated with artifacts, such as tools, e.g., an abacus, or inscribed representations, e.g., an equation (Alibali, Flevares, & Goldin-Meadow, 1997), whether or not these artifacts are physically present. That is, gesturing, like interaction with physically present mathematical artifacts, transpires within the spatial medium, and so gestures associated with mathematical artifacts may evince spatial features of these interactions, revealing aspects of the artifacts that the person is attending to as significant for a problem at hand. It follows that some aspects of mathematical reasoning are grounded as manipulations of imaged artifacts (Presmeg, 2006). Thus, the routinization of practice with physical mathematical artifacts renders them embodied constructions (Hatano, Miyake, & Binks, 1977; Verillon & Rabardel, 1995; Vygotsky, 1978/1930).
In the case of artifacts that are new to a problem solver - a typical scenario in design-based research studies - gesture may uniquely reveal conceptual construction in action, such as when a student interacting with the artifacts builds connections among personal resources (Case & Okamoto, 1996). Thus, in studying learners' gesture-based interactions with mathematical artifacts under development, I investigate the nature of multimodal resources these artifacts afford. What developmental trajectories do these artifacts enable toward appropriation of normative mathematical forms? What limitations might the artifacts be imposing on students' expressivity? What design-theory principles do the data suggest in terms of developing effective learning tools?
Earlier, the LF data served as context for explaining ontological imperialism and its pedagogical problematics. The dilemma concerned the question of how to preempt such imperialism yet shepherd students into convergence with normative mathematics. To do so, I am suggesting, we should listen closely to students' embodied presymbolic ontology and create cognitively ergonomic mathematical learning tools, i.e., artifacts aligned with, and hence affording, students' embodied reasoning. At the same time, these tools should "surreptitiously include mathematical features inviting elaboration. Following, the MK data will serve as context to demonstrate this method, which I call embodied design (cf. Van Rompay & Hekkert, 2001).
5. A Case of Coping With the Obduracy of the World (and How a Designer Tried to Improve This World
MK, a senior statistics major, has been working with 4-Blocks, a computer-based simulation of the marbles-scooper experiment, with the p value set at .5 (see Applet 1, below). An on-screen histogram, which tracks the accumulation of outcomes, has converged, over thousands of trials, closely upon the expected 1-4-6-4-1 distribution.
[The applet requires Java 1.4.1 or higher. It will not run on Windows 95 or Mac OS 8 or 9. Mac users must have OS X 10.2.6 or higher and use a browser that supports Java 1.4. (Safari works, IE does not. Mac OS X comes with Safari. Open Safari and set it as your default web browser under Safari/Preferences/General.) On other operating systems, you may obtain the latest Java plugin from Sun's Java site
Applet 1. The 4-Blocks simulation of the marbles-box probability experiment NetLogo model. To interact with other ProbLab models not discussed in the paper, go here.
Int. asks MK what the distribution might be for p values higher than the default .5. MK replies:
It would be... If it was more likely to be green, it would be skewed (see Figure 3a)... This [right-side histogram columns in the 4-Blocks simulation] would get bigger, this [left-side column] would get smaller...

| a | b | c | d | e | f |
Figure 3. Negotiating media constraints on image expressivity, MK: (a) manipulates the on-screen histogram "hands off" to indicate the expected histogram for a p value of .6; (b) manipulates the on-screen histogram "hands on"; (c) considers pen and paper, but declines; (d) manipulates the on-screen histogram "hands on" remotely, using the combinations tower; (e) shifts up the right-most single card to show the expected shape (compare to Figure 3b); but (f) returns the card because the shift violated constraints of the representational form.
Recognizing that she cannot manipulate the on-screen histogram directly, MK remote-manipulates it. First, she frames the histogram - her gaze peering through her hands toward the screen yet not focusing on the transparent plain subtended by her hands and tilts the histogram to the right (see Figure 3a). Next, she touches the screen itself, calibrating histogram columns up and down to adjust it (see Figure 3b). Unsatisfied, she then turns away from the screen, and her right hand hovers momentarily over a pen (see Figure 3c), as though she means to sketch the expected histogram upon the available sheet of paper. But she abandons that medium and turns to the combinations tower on the desk, saying: "but it would shift, like...," (see Figure 3d). Moving her hands in opposite vertical directions - left hand down, right hand up - she has actually made the 1-column shorter and the 3-column taller. Now she turns to the single card on the right of the tower, wishing to show that this 4-green column, too, would become taller. She lays her right hand on the card and pushes it "up to the desired height (see Figure 3e). Yet, once up there, this single card no longer aligns with the bottom of the tower so MK returns the card to its original location (Figure 3f), stating that the card medium ultimately limits her in expressing her mathematical reasoning: "You can't really do it on these cool things [cards], but it would be more like that.""
It appears, thus, that the semiotic means of objectification available to MK constrained her expressivity. These observations of student behavior directly informed subsequent design. Namely, I created Histo-Blocks (see below) to enable student expression of expected outcome distributions for literally any p value as transformation on the sample space, the very transformation that MK attempted yet, as we saw, turns out to be either imprecise or impossible in the physical space.
6. Histo-Blocks: From an Obdurate Physical World to an Accommodating Electronic World
Histo-Blocks (see Figure 4) is a computer-based interactive visualization designed to foster deep understanding of the binomial function by enabling electronically the gestures students were observed to attempt physically on the sample space. The model also enhances the expressivity, vividness, and precision of the transformations. The binomial function expresses the probability of sampling a particular combination, for instance any 4-block with exactly three green squares, for given chances of getting a green square, say .6 (as when 60% of the marbles are green). In order to help students understand the binomial formula, its two factors - combinatorics and chance - have been conceptually decoupled, as in the binomial function, and distributed over unique yet interlinked interface elements (see, in Figure 4, three monitors on the bottom left - the bottom one displays the product of the two above it).
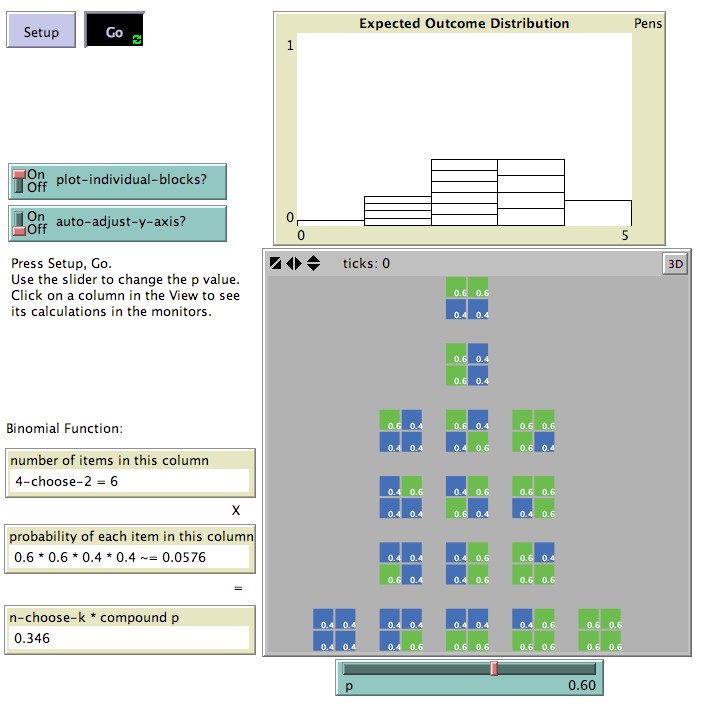
Figure 4. Interface of ProbLab model
Histo-Blocks, built in NetLogo. In this screen-shot, the function,
histogram, and monitors all express properties of the middle column of
the combinations tower for p=.6. The middle column in the
stratified histogram directly above the tower is equal in height
to the column immediately adjacent to its right, because the properties
of these two columns are
6 * 0.6 * 0.6 * 0.4 * 0.4 = ~.346
4 * 0.6 * 0.6 * 0.6 * 0.4 = ~.346
respectively (see in
the monitors; note how the '4' and '6' compensate for each
other).
Applet 2. The Histo-Blocks theoretical-probabilty NetLogo model (not an empirical simulation).
Manipulating the "p" slider (see in Applet 2, under the tower) directly redistributes the total area of the expected outcome distribution in the histogram (above the tower), just as MK attempted to do with the cards (the physical embodiment of the combinations-tower). Yet, unlike the cards, the elements of each column in the Histo-Blocks histogram are given to simultaneous and precise stretching and shrinking—uniform within columns, variable between columns—in response to a single manipulation of the p slider. Pertinently, note how the entire 4-green column in the histogram is stretched up without losing its base as it did for MK. Thus, Histo-Blocks enables learners to manipulate the sample space (the combinations tower) so as to express the outcome distribution they anticipate to recieve in actual experiments. In the later interviews of our study, we had opportunities to engage several students in pilot activities in which they successfully coordinated the physical combinations tower with elements of the Histo-Blocks simulation (Abrahamson, in 2008a).
7. Summary Remarks: Deep Learning as Creative Response to Breakdown
A major challenge of mathematical learning is to develop fluency with its notational system. Leading scholars operating in the contexts of embodied reasoning, techo-science, and cultural semiotics have pointed to the rupture (Radford, 2003) students experience as they ford the topological-typological hiatus (Lemke, 1998) between embodied presymbolic notions and normative forms of inscribed expression. Yet, whereas cultures have evolved artifacts that mind the embodied-symbolical gap (e.g., the clock, Collins & Ferguson, 1993; Hutchins, 2005), mathematics-education designers - who cannot wait millennia for the survival of the fittest instructional materials - need design principles to help students ground mathematical notation today. The electronic medium offers a potentially powerful space for students to develop such coordination through manipulating interlinked spatial and symbolical representations (e.g., Kaput & West, 1994), and operating within the design-based research paradigm has enabled researchers to carefully select or create interactive media tailored to the domain-specific understandings of the target clients. In this paper I have proposed that an embodied-cognition perspective on mathematical reasoning may offer a powerful lens on video data of students engaging in situated problem solving—a lens that is complementary to traditional focus on verbal utterance only. In particular, identifying moments of students' truncated embodied expression can alert designers to the absence of appropriate semiotic means of objectification, which they can then create and make available to learners.
However, a designer's quest to streamline the learning environment such that it afford students tacit appropriation of representational forms may compete with a pedagogical principle that students should reflect on the procedures they are adopting. In fact, two classical constructs - Heidegger's 'breakdown' and Piaget's 'reflective abstraction' - are akin inasmuch as they both focus on moments of disruption in the flow of action as engendering constructive consideration of the equipment at hand, be it mechanical or epistemic (see Abrahamson in-press; cf. Koschmann, Kuuti, & Hickman, 1998). I identify a continuum between these mundane moments of reflection and monumental moments of creativity. Thus, designing content-targeted learning tools that both trigger students' experiences of the obduracy of the world and structure their appropriation of prepared solutions may enable learners to progress within the discipline of mathematics and practice creative problem-solving. Namely, usability per se, such as through avoidance of ambiguity, need not necessarily be the golden standard in educational design as it is in industrial design (cf. Norman, 2002). Rather, educational design is to some extent a craft of tradeoffs between usability and pedagogy. For example, by virtue of facilitating students electronic manipulation of the combinations-tower columns, I am liable to deny students opportunities to reflect on the media and content. Perhaps it was important that MK manipulated the obdurate cards physically before working with the computer-based model - perhaps she learned by ensuring that the middle column becomes shorter so as to compensate for the growth of the columns to its right?1
1 I wish to thank Joey Relaford-Doyle for our ongoing dialogue that helps me understand these challenging data.
References
Abrahamson, D. (2004). Keeping meaning in proportion: The multiplication table as a case of pedagogical bridging tools. Unpublished doctoral dissertation. Northwestern University, Evanston, IL.
Abrahamson, D. (2006a). Learning chance: Lessons from a learning-axes and bridging-tools perspective. In A. Rossman & B. Chance (Eds.), Proceedings of the Seventh International Conference on Teaching of Statistics. Salvador, Bahia, Brazil.
Abrahamson, D. (2006b). The shape of things to come: The computational pictograph as a bridge from combinatorial space to outcome distribution. International Journal of Computers for Mathematical Learning, 11(1), 137-146.
Abrahamson, D. (2007a). From intuition to inscription: Emerging design principles for mathematics education. Paper presented at the annual meeting of the International Society for Design and Development in Education (ISDDE), Berkeley, CA, September 17 - 21.
Abrahamson, D. (2007b). The real world as a trick question: Undergraduate statistics majors' construction-based modeling of probability. Paper presented at the annual meeting of the American Education Research Association, Chicago, IL.
Abrahamson, D. (2007c). Handling problems: Embodied reasoning in situated mathematics. In T. Lamberg & L. Wiest (Eds.). Proceedings of the Twenty Ninth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 219-226). Stateline (Lake Tahoe), NV: University of Nevada, Reno.
Abrahamson, D. (in 2008a). Embodied design: Constructing means for constructing meaning. Educational Studies in Mathematics. .
Abrahamson, D. (in 2008b). Probability by design: Synthesizing event-based intuition and outcome-based analysis. Cognition and Instruction . (Manuscript under revision) .
Abrahamson, D. (in-press). Bridging theory: A case study of an 11-year-old student engaged in activities designed to support the grounding of outcome-based combinatorial analysis in event-based intuitive judgment. In M. Borovcnik & D. Pratt (Eds. of Topic Study Group 13, Research and Development in the Teaching and Learning of Probability), in the Proceedings of the International Congress on Mathematical Education (ICME 11). Monterrey, Mexico: ICME.
Abrahamson, D., Bryant, M. J., Howison, M. L., & Relaford-Doyle, J. J. (2008). Toward a phenomenology of mathematical artifacts: A circumspective deconstruction of a design for the binomial . Paper presented at the annual conference of the American Education Research Association, New York, March 24-28.
Abrahamson, D., & Cendak, R. M. (2006). The odds of understanding the law of large numbers: A design for grounding intuitive probability in combinatorial analysis. In J. Novotná, H. Moraová, M. Krátká, & N. Stehlíková (Ed.), Proceedings of the Thirtieth Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 1 - 8). Prague, Czech Republic: Charles University.
Abrahamson, D., & Wilensky, U. (2002). ProbLab . Northwestern University, Evanston, IL: The Center for Connected Learning and Computer-Based Modeling, Northwestern University.
Abrahamson, D., & Wilensky, U. (2007). Learning axes and bridging tools in a technology-based design for statistics. International Journal of Computers for Mathematical Learning, 12 (1), 23-55.
Alibali, M. W., Bassok, M., Olseth, K. L., Syc, S. E., & Goldin-Meadow, S. (1999). Illuminating mental representations through speech and gesture. Psychological Science, 10, 327-333.
Alibali, M. W., Flevares, L. M., & Goldin-Meadow, S. (1997). Assessing knowledge conveyed in gesture: Do teachers have the upper hand? Journal of Educational Psychology, 89(1), 183-193.
Bamberger, J., & diSessa, A. A. (2003). Music as embodied mathematics: A study of a mutually informing affinity. International Journal of Computers for Mathematical Learning, 8(2), 123-160.
Barab, S., Zuiker, S., Warren, S., Hickey, D., Ingram-Goble, A., Kwon, E.-J., et al. (2007). Situationally embodied curriculum: Relating formalisms and contexts. Sci Ed (Wiley InterScience), 91, 750-782.
Barsalou, L. W. (1999). Perceptual symbol systems. Behavioral and brain sciences, 22, 577-660.
Brown, A. (1992). Design experiments: Theoretical and methodological challenges in creating complex interventions in classroom settings. Journal of the Learning Sciences, 2(2), 141-178.
Case, R., & Okamoto, Y. (1996). The role of central conceptual structures in the development of children's thought. In Monographs of the society for research in child development: Serial No. 246 (Vol. 61). Chicago: University of Chicago Press.
Cobb, P., & Bauersfeld, H. (Eds.). (1995). The emergence of mathematical meaning: Interaction in classroom cultures . Hillsdale, NJ: Lawrence Erlbaum.
Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9-13.
Collins, A. (1992). Towards a design science of education. In E. Scanlon & T. O'shea (Eds.), New directions in educational technology (pp. 15-22). Berlin: Springer.
Collins, A., & Ferguson, W. (1993). Epistemic forms and epistemic games: Structures and strategies to guide inquiry. Educational Psychologist, 28 (1), 25-42.
Confrey, J. (1991). Learning to listen: A student's understanding of powers of ten. In E. v. Glassersfeld (Ed.), Radical constructivism in mathematics education (pp. 111-138). Dordrecht, The Netherlands: Kluwer Academic Publishers.
Confrey, J. (2005). The evolution of design studies as methodology. In R. K. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 135-151). Cambridge, MA: Cambridge University Press.
Ernest, P. (1988). Social constructivism as a philosophy of mathematics Albany, NY: SUNY Press.
Fauconnier, G., & Turner, M. (2002). The way we think: Conceptual blending and the mind's hidden complexities. New York: Basic Books.
Gee, J. P. (1996). Social linguistics and literacies: Ideology in discourses (2nd ed.). London: Taylor & Francis.
Ginsburg, H. P. (1997). Entering the child's mind. New York: Cambridge University Press.
Goodwin, C. (1994). Professional vision. American Anthropologist, 96 (3), 603-633.
Hatano, G., Miyake, Y., & Binks, M. (1977). Performance of expert abacus operators. Cognition, 5, 57-71.
Hutchins, E. (2005). Material anchors for conceptual blends. Journal of Pragmatics, 37(10), 1555-1577.
Jones, G. A., Langrall, C. W., & Mooney, E. S. (2007). Research in probability: Responding to classroom realities. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 909 - 955). Charlotte, NC: Information Age Publishing.
Kaput, J., & West, M. M. (1994). Missing-value proportional reasoning problems: Factors affecting informal reasoning patterns. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 237-287). Albany, NY: SUNY.
Kendon, A. (2004). Gesture: Visible action as utterance Cambridge, UK: Cambridge University Press.
Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist, 41 (2), 75-86.
Koschmann, T., Kuuti, K., & Hickman, L. (1998). The concept of breakdown in Heidegger, Leont'ev, and Dewey and Its implications for education. Mind, Culture, and Activity, 5(1), 25-41.
Lemke, J. L. (1998). Multiplying meaning: Visual and verbal semiotics in scientific text. In J. R. Martin & R. Veel (Eds.), Reading science: Critical and functional perspectives on discourses of science (pp. 87-113). London: Routledge.
McNeill, D. (1992). Hand and mind: What gestures reveal about thought Chicago: University of Chicago Press.
Merleau-Ponty, M. (1992). Phenomenology of perception (C. Smith, Trans.). New York: Routlidge.
Norman, D. A. (2002). The design of everyday things . New York: Basic Books.
Olson, D. R. (1994). The world on paper. Cambridge, UK: Cambridge University Press.
Presmeg, N. (2006). Research on visualization in learning and teaching mathematics: Emergence from psychology. In A. Gutierrez; P. Boero (Eds.), Handbook of research on the psychology of mathematics education: Past, present, and future (pp. 205-235). Rotterdam: Sense Publishers.
Radford, L. (2003). Gestures, speech, and the sprouting of signs: A semiotic-cultural approach to students' types of generalization. Mathematical Thinking and Learning, 5(1), 37-70.
Rizzolatti, G., & Arbib, M. A. (1998). Language within our grasp. Trends in Neurosciences, 21(5), 188-194.
Rotman, B. (2000). Mathematics as sign: Writing, imagining, counting style='font-size:10.0pt; color:black'>. Stanford, CA: Stanford University Press.
Sawyer, R. K. (2007). Group genius: The creative power of collaboration style='font-size:10.0pt; color:black'>. New York: Perseus Books Group.
Saxe, G. B. (1981). Body parts as numerals: A developmental analysis of numeration among the Oksapmin in Papua New Guinea. Child Development, 52 (1), 306-331.
Schegloff, E. A. (1984). On some gestures' relation to talk In J. M. Atkinson & E. J. Heritage (Eds.), Structures of Social Action: Studies in Conversation Analysis (pp. 266-296). Cambridge: Cambridge University Press.
Schön, D. A. (1981). Intuitive thinking? A metaphor underlying some ideas of educational reform (Working Paper 8): Division for Study and Research, M.I.T.
Siegler, R. S., & Crowley, K. (1991). The microgenetic method: a direct means for studying cognitive development. American Psychologist, 46 (6), 606-620.
Stevens, R., & Hall, R. (1998). Disciplined perception: Learning to see in technoscience. In M. Lampert & M. L. Blunk (Eds.), Talking mathematics in school: Studies of teaching and learning (pp. 107-149). New York: Cambridge University Press.
Van Rompay, T., & Hekkert, P. (2001). Embodied design: on the role of bodily experiences in product design. In Proceedings of the International Conference on Affective Human Factors Design (pp. 39-46). Singapore.
Varela, F. J., Thompson, E., & Rosch, E. (1991). The embodied mind: Cognitive science and human experience. Cambridge, MA: M.I.T. Press.
Vérillon, P., & Rabardel, P. (1995). Cognition and artifacts: A contribution to the study of thought in relation to instrumented activity. European Journal of Psychology of Education, 10 (1), 77-101.
von Glasersfeld, E. (1992). Aspects of radical constructivism and its educational recommendations (Working Group #4). Paper presented at the Seventh International Congress on Mathematics Education (ICME7), Quebec.
Vygotsky, L. S. (1978/1930). Mind in society: The development of higher psychological processes. Cambridge: Harvard University Press.
Wilensky, U. (1997). What is normal anyway?: Therapy for epistemological anxiety. Educational Studies in Mathematics, 33 (2), 171-202.
Wilensky, U. (1999). NetLogo. Northwestern University, Evanston, IL: The Center for Connected Learning and Computer-Based Modeling .
Wittgenstein, L. (1956). Remarks on the foundations of mathematics . UK: Basil Blackwell.

